Wissen
Was ist eigentlich das Vega?
Jeder Optionsschein-Anleger sollte grundsätzlich wissen, wie der Optionspreis auf die Veränderung des zugrunde liegenden Basiswerts reagiert. Dieses Thema wurde bereits in den vergangenen zwei Ausgaben des ideas-Magazins ausführlich erörtert. Ein weiterer wichtiger Faktor, der den Optionspreis beeinflusst, ist die Volatilität.
Die Volatilität ist die Standardabweichung der Veränderungen des Basiswertkurses und beschreibt somit die Intensität der Basiswertkursschwankungen. Misst man diese Standardabweichung aus den Zeitreihen historischer Basiswertänderungen, dann spricht man von historischer Volatilität. Die Bewertung einer Option erfordert allerdings nicht die historische, sondern die erwartete Schwankungsbreite eines Basiswerts. Sie wird implizite Volatilität genannt und kann bei gegebenen Optionspreisen an einem Terminmarkt sogar auch berechnet werden. Hohe Volatilität bedeutet hohe Wahrscheinlichkeit für stärkere Kursschwankungen. Das bedeutet wiederum intuitiv, dass die Wahrscheinlichkeit steigt, dass ein Optionsschein (sowohl Call als auch Put) sich in die vom Anleger gewünschte Entwicklung bewegt, was den Optionsscheinwert erhöhen sollte.
Der Einfluss der (impliziten) Volatilität auf den Optionspreis wird mit der Kennzahl Vega gemessen. Das Vega gibt an, um wie viel Euro sich der Wert eines Optionsscheins ändert (bereinigt um das Bezugsverhältnis), wenn die implizite Volatilität um 1 Prozentpunkt steigt oder fällt. Das Vega ist immer positiv und lässt sich als die partielle Ableitung des Optionsscheinpreises nach der impliziten Volatilität sowohl für Plain Vanilla Calls als auch für Puts mit einer positiven Restlaufzeit ermitteln. Das heißt auch, wie vorher intuitiv angenommen, je höher die Volatilität ist (wenn alle anderen Einflussgrößen unverändert bleiben), umso höher ist der Preis eines Optionsscheins.
Wie man Vega interpretiert, lässt sich anhand des folgenden Beispiels zeigen.
Beispiel
Der Call Optionsschein auf die ABC-Aktie mit einem Basispreis von 50 Euro und einer Laufzeit bis zum 21. März 2025 hatte am 22. November 2024 bei einem Kurs der ABC-Aktie von 48 Euro einen theoretischen Wert von 2,56 Euro. Dies entspricht bei einer impliziten Volatilität von 30 Prozent einem Vega von 0,12. In diesem Fall kann angenommen werden, dass der Wert des Optionsscheins um 12 Eurocent auf 2,68 Euro ansteigt, falls die implizite Volatilität auf 31 Prozent steigt. Steigt die Volatilität auf 32 Prozent, würde sich der Call-Wert auf 2,80 Euro erhöhen (2,56 + 2 x 0,12). Genauso ist mit einem Wertverlust des Calls von 2,56 auf 2,44 Euro zu rechnen, falls die Volatilität um 1 Prozentpunkt auf 29 Prozent fällt.
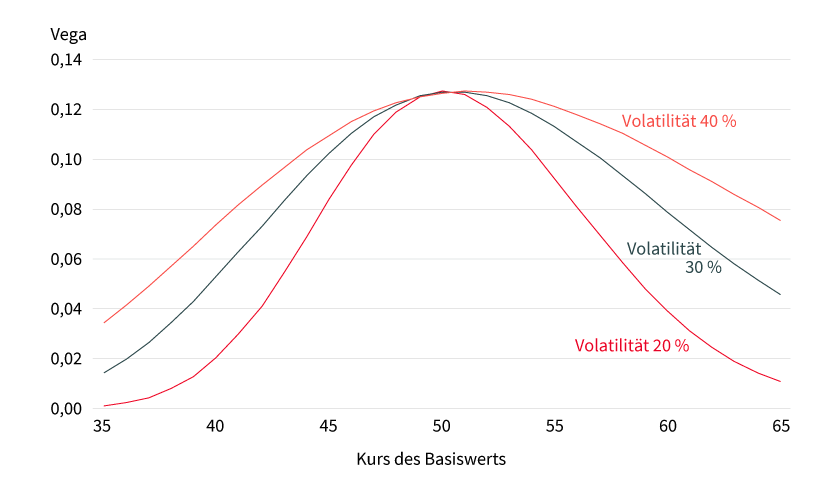
Analog zu Delta und Gamma ist auch Vega eine dynamische Größe und stellt eine Momentaufnahme dar. Die nebenstehende Grafik zeigt Vega-Werte in Abhängigkeit vom Kurs des Basiswerts für den Call auf die ABC-Aktie, fällig am 21. März 2025 für drei verschiedene Volatilitätsniveaus: 20 Prozent, 30 Prozent und 40 Prozent. Es gilt generell, dass der absolute Vega-Einfluss am größten ist, wenn ein Optionsschein am Geld liegt, das heißt der aktuelle Basiswertkurs nah am Basispreis ist. Des Weiteren gilt, je höher der Volatilitätslevel ist (bei allen anderen unveränderten Einflussfaktoren), desto höher ist das Vega und umso stärker reagiert ein Optionsschein auf Veränderung der Volatilität. Auch die steigende Restlaufzeit erhöht den absoluten Vega-Level.
Bei weit aus dem Geld stehenden Optionsscheinen ist dennoch Vorsicht geboten. Auch wenn sie ein geringes Vega ausweisen, ist es in Relation zum Optionsscheinwert höher, sodass solche Optionsscheine prozentual stärker auf Volatilitätsveränderung reagieren. Der bereits beschriebene Call auf die ABC-Aktie würde am 22. November 2024 bei einem Aktienkurs von 40 Euro bei 0,39 Euro notieren und hätte ein Vega von 0,05. Der Volatilitätsanstieg von 1 Prozentpunkt würde den Call-Preis um 13 Prozent auf 0,44 Euro erhöhen. Die Beispiele verdeutlichen, dass neben der Bewegung des Basiswerts (der Aktie oder des Index) selbst, auf den sich der Optionsschein bezieht, auch die alleinige Bewegung der Volatilität nicht zu vernachlässigen ist, da sie einen signifikanten Einfluss auf die Preisveränderung eines Optionsscheins haben kann. Das ist insbesondere in volatilen Marktphasen der Fall.